2. Etapas da modelagem de equações estruturais (SEM) com AMOS

O arquivo de dados brutos a ser analisado é aberto selecionando o local onde o arquivo é salvo na janela que se abre com a opção Arquivos de dados → Nome do arquivo no menu Arquivo na janela principal do AMOS Graphics. O software AMOS pode abrir arquivos de dados SPSS, Excel, MS Access, Lotus e Dbase. Como alternativa ao menu Arquivo, o mesmo pode ser feito clicando  no ícone na barra de ferramentas. Depois de selecionar o arquivo de dados, o nome do arquivo de dados e o número de dados podem ser exibidos na janela "Arquivos de dados". Abaixo está uma captura de tela mostrando o nome do arquivo de dados e o número de dados.

Como visto na Figura 7, o arquivo de dados chamado "Emotion Regulation" consiste em 332 dados.

É necessário um teste de normalidade antes de as equações serem definidas. Depois de selecionar o arquivo de dados a ser analisado na tela AMOS Graphics, as variáveis observadas a serem incluídas na análise são selecionadas na janela "Variáveis no conjunto de dados" aberta com a opção "listar variáveis no conjunto de dados"  e transferidas para a tela de trabalho no lado direito, arrastando e soltando com o mouse. As estatísticas descritivas podem ser feitas clicando no ícone relevante ou através da opção "Propriedades de Análise" acedida através do menu. Os valores do mínimo e do máximo, bem como a curtose univariada e a assimetria, estão incluídos nestas estatísticas descritivas. Os valores de distância de Mahalanobis são fornecidos por outliers, que identificam os dados que estão mais distantes do centro (Byrne, 2001). Na guia "Saída", selecione a opção "Teste de normalidade e valores atípicos". 

Após a seleção, a janela é fechada. Clique em "Calcular estimativas" ou no ícone  do menu "Analisar". Para visualizar os resultados, clique em "Saída de texto" no menu "Ver" ou no  ícone. Na janela "AMOS Output", clique em "Avaliação da normalidade" e os resultados são exibidos.  A suposição de normalidade é determinada pelo "coeficiente de Mardia" no programa de software AMOS.

No cálculo, aplica-se a fórmula p*(p+2), onde p é o número total de variáveis observadas (Raykov & Marcoulides, 2008). Os dados podem ser considerados normais multivariados se o coeficiente de Mardia for inferior ao valor derivado da fórmula (Khine, 2013). Por exemplo, em um modelo com duas variáveis observadas, o coeficiente de Mardia deve ser inferior a oito (Raykov & Marcoulides, 2008). Se o pressuposto de normalidade não puder ser cumprido, identificar valores anómalos e excluí-los do conjunto de dados pode ser uma forma alternativa de assegurar o pressuposto.

Após o cumprimento do pressuposto de normalidade, o modelo estrutural é construído de acordo com as hipóteses da pesquisa. A variável latente e suas variáveis observadas são desenhadas no espaço de trabalho à direita, clicando no  ícone do menu do lado esquerdo. As variáveis observadas são selecionadas a partir da janela aberta clicando no  ícone e transferidas para a tela arrastando e soltando com o mouse. As variáveis latentes são representadas por elipses, enquanto as variáveis observadas são representadas por retângulos. Os valores de erro associados às variáveis observadas também são mostrados como elipses e todas as variáveis observadas têm valores de erro. A figura abaixo mostra a variável latente, as variáveis observadas e os valores de erro dessas variáveis observadas na janela principal do AMOS Graphics. 

Na Figura 8, "Mindfulness" é a variável latente, "MAAS1" e "MAAS2" são variáveis observadas, "e1" e "e2" são valores de erro. De acordo com esta figura, a Mindful Attention Awareness Scale (MAAS; Castanho e Ryan, 2003; Özyeşil et al., 2011), que mede mindfulness, consiste em duas subdimensões determinadas pelo método de parcelamento: MAAS1 e MAAS2. De acordo com o número de variáveis latentes utilizadas no modelo, o diagrama é selecionado com o  ícone e copiado com o  ícone.

Uma avaliação de quão bem as variáveis observadas representam a variável latente que supostamente medem é possibilitada pelo modelo de medição (Gallagher et al., 2008). Para elaborar o modelo de medição, a variável latente e as variáveis observadas são conectadas por uma seta unidirecional . Além disso, a covariância é desenhada entre as variáveis latentes. Um exemplo de modelo de medição é dado abaixo (O modelo de medição no exemplo tem duas variáveis latentes e é criado apenas para fins de exemplo. No entanto, todas as variáveis latentes no seu modelo serão incluídas no modelo de medição e a covariância será desenhada entre todas as variáveis latentes).   

A Figura 9 mostra o modelo de medição constituído pela variável independente "Mindfulness", a variável dependente "Emotion Regulation" e as subdimensões destas variáveis. Depois de criar o modelo de medição, selecione o ícone no menu do lado esquerdo da tela. Nesta tela, as caixas "índices de modificação", "estimativas padronizadas" e "efeitos diretos e indiretos" devem ser marcadas. Depois de fechar a janela de propriedades de análise, clique no ícone "Calcular estimativas"  e execute o cálculo. Selecione o ícone "Ver texto"  na barra de ferramentas para abrir o arquivo de saída. No modelo de medição, as cargas fatoriais devem ser examinadas primeiro. Na janela "Saída", selecione "Estimativas" na lista à esquerda. Com significância estatística, as cargas fatoriais padronizadas devem ser superiores a .50 e, idealmente, superiores a .70 (Hair et al., 2019). Depois de avaliar as cargas fatoriais, o ajuste geral do modelo deve ser examinado através da bondade dos índices de ajuste fornecidos sob o título "Ajuste do modelo". Os critérios de corte dos índices de ajuste recomendados por Schermelleh-Engel et al (2003) são apresentados na Tabela 1.  

Abaixo está uma imagem de saída de exemplo com a bondade dos índices de ajuste.

Quando comparados com os critérios de corte dos índices de ajuste da Tabela 1, GFI=.978, AGFI=.944, NFI=.975 e TLI=.973 são avaliados entre os critérios de "bom ajuste". Espera-se que a bondade dos índices de ajuste do modelo de medição esteja dentro da faixa de critérios de ajuste bom ou aceitável. O modelo estrutural deve ser testado após a avaliação da bondade dos índices de ajuste do modelo de medição.

Depois de desenhar o diagrama, as variáveis endógenas e exógenas devem ser conectadas entre si com uma seta unidirecional . Os erros das variáveis endógenas são incluídos no modelo clicando na variável com o ícone "Adicionar uma variável única a uma variável existente".  Plugins → Nomeie variáveis não observadas para nomear essas variáveis (se a nomeação não for feita, um aviso aparecerá durante a fase de análise). Apresenta-se seguidamente um modelo estrutural de exemplo.

Uma das hipóteses do modelo de equações estruturais apresentado na Figura 11 é "A ligação entre a atenção plena dos pais e a regulação emocional dos filhos é mediada pela atenção plena no casamento". Com base nessa hipótese, a atenção plena dos pais prevê a atenção plena no casamento e a atenção plena no casamento prevê a regulação emocional de seus filhos. Assim, pode-se dizer que a atenção plena dos pais prevê a regulação emocional de seus filhos através da atenção plena no casamento. Se você tentar analisar o modelo estrutural na figura, verá um aviso sobre a não inclusão de termos de erro.  Portanto, adicionar um termo de erro às variáveis endógenas (dependentes) é importante.

Uma vez concluído o modelo estrutural, seguem-se as etapas de teste do modelo de medição descrito na seção anterior. Em primeiro lugar, deve examinar-se se as estimativas dos parâmetros são estatisticamente significativas. Na janela "Saída", selecione "Estimativas" na lista à esquerda. Efeitos diretos, indiretos e totais podem ser vistos na tela que se abre após a seleção. Coeficientes de caminho significativos são importantes para o ajuste geral do modelo (Baron & Kenny, 1986). O coeficiente de regressão deve ser verificado quanto à significância dos coeficientes de trajetória. Para examinar se esses valores são significativos ou não, o  valor de p de cada um deles deve ser examinado. Se este valor for inferior a .05, pode-se dizer que o coeficiente de caminho é significativo. Abaixo está uma imagem de saída de amostra mostrando os coeficientes de regressão e coeficientes de regressão padronizados. 

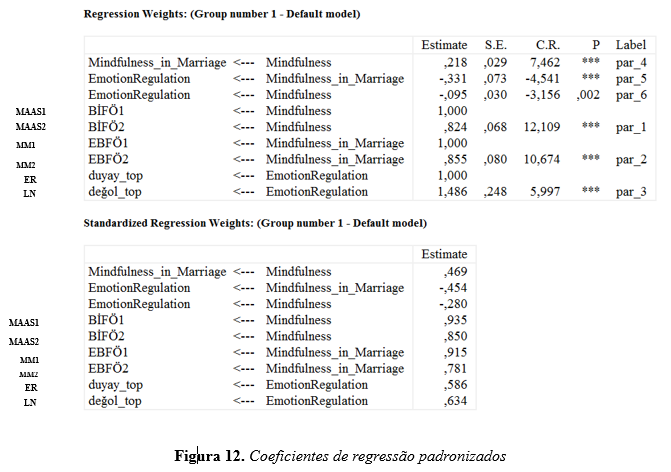
Na Figura 12, em primeiro lugar, deve-se examinar se os coeficientes de caminho são significativos ou não na tabela "Pesos de Regressão". A tabela "Pesos de Regressão Padronizados" deve ser examinada quanto aos coeficientes de caminho. Embora seja desejável para o modelo que todos os caminhos sejam significativos, a não significância do caminho entre a variável dependente e a variável independente não é vista como um problema, uma vez que reflete a força da variável mediadora na relação. Depois de avaliar se os coeficientes de caminho são significativos ou não, a bondade dos índices de ajuste fornecidos sob o título "Model Fit" no arquivo de saída são examinados e avaliados de acordo com os critérios de corte dos índices de ajuste. Os modelos com melhor ajuste aos dados são indicados pela bondade dos índices de ajuste (Smith & McMillan, 2001). A bondade dos índices de ajuste é avaliada no âmbito dos critérios de corte dos índices de ajuste recomendados por Schermelleh-Engel et al (2003) e apresentados na Tabela 1.  Em resultado destas avaliações, o modelo estrutural é aceite, rejeitado ou modificado.  

Depois de examinar os índices de ajuste, modificações no modelo podem ser feitas para um melhor ajuste do modelo. Os índices de modificação sugerem que essas alterações sejam feitas. No entanto, deve-se ter cuidado ao fazer modificações e cada modificação no modelo deve ser baseada em uma base teórica. Como resultado, o pesquisador deve explicar por que a mudança foi feita e se ela é teoricamente significativa para o modelo (Schreiber et al., 2006).

Dado que o único grau de liberdade do valor da tabela qui-quadrado é 3,84 (Whittaker, 2012), 4 é usado como o valor de corte dos índices de modificação. Se não houver índices de modificação como resultado da análise, não há valor que exceda o valor de corte. Abaixo está uma imagem de saída com os índices de modificação sugeridos após o teste do modelo.

Na imagem acima, os índices de modificação entre os valores de erro e1 e e5 são calculados como 4,123. Assim, recomenda-se desenhar a covariância entre esses dois valores de erro e testar novamente o modelo. Uma vez que as modificações tenham sido teoricamente avaliadas (as modificações devem ser teoricamente fundamentadas) e feitas, o modelo deve ser testado novamente. Se forem obtidos índices de ajuste bons ou aceitáveis após o modelo ser novamente testado, o modelo é aceite; caso contrário, o modelo deve ser modificado novamente, se possível. O processo de modificação é continuado até que uma nova modificação não possa ser feita e o modelo seja aceito ou rejeitado de acordo com os índices de ajuste obtidos devido a essas modificações.

A última etapa da Modelagem de Equações Estruturais é determinar a validade do modelo. Um dos métodos mais comuns usados para determinar a validade do modelo estrutural é o método "Bootstrapping". O processo de bootstrapping consiste na reamostragem dos dados originais (Scharkow, 2017). Utilizando esta estratégia, podemos verificar a validade do modelo em amostras maiores. Para bootstrapping, o item de menu "Propriedades de análise" é aberto e a seção "Efeitos indiretos, diretos e totais" é selecionada.  Na guia "Bootstrap", as opções "Perform Bootstrap", "Bias-Corrected Confidence Intervals" e "Bootstrap ML" são selecionadas. Digite um número entre 500 e 1000 para a opção "Número de amostras de bootstrap" (Cheung & Lau, 2008). Este número representa o número de reamostragem do seu modelo. Escreva 95 para a opção "Nível de confiança BC". Assim, a análise é realizada com um intervalo de confiança de 95%. Depois de tudo ter sido feito até agora, clique no botão "Calcular Estimativas" e obtenha os resultados. Um exemplo de captura de tela do menu "Propriedades de análise" é dado abaixo.

A guia "Efeito Indireto Padronizado" em Saída mostra o efeito indireto da variável independente sobre a variável dependente.  Se este efeito é significativo é determinado olhando para os limites inferior e superior do intervalo de confiança. Para isso, o número entre a variável independente e a variável dependente deve ser verificado nas tabelas "Limites Inferiores" e "Limites Superiores" na guia "Efeito Indireto Padronizado". Estes números representam o limite inferior e o limite superior do intervalo de confiança. Hayes (2022) afirmou que um efeito indireto é significativo se não houver zero entre os limites inferior e superior do intervalo de confiança (por exemplo, o limite inferior é -.470 e o limite superior é -.102). A captura de tela mostrando o limite inferior e o limite superior na tabela é dada abaixo.

Na Figura 15, como nossa variável independente é "Mindfulness" e nossa variável dependente é "Emotion Regulation", quando olhamos para os valores de limite inferior (-.470) e superior (-.102) entre essas duas variáveis, vemos que não há zero entre elas. Assim, como resultado do bootstrapping, o efeito indireto no modelo estrutural é significativo em um intervalo de confiança de 95%. No final, todas as análises conduzidas no âmbito da Modelação de Equações Estruturais devem ser reportadas.