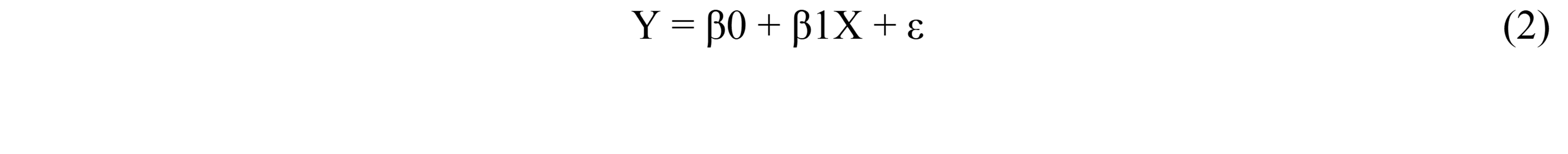Summary: Introduction to regression analysis, its purpose, basic concepts, and types.
Understand the concept of regression analysis and its applications in modeling relationships between variables.
Learn about different types of regression analysis, including simple linear regression and multiple regression.
Identify scenarios where regression analysis is appropriate and interpret regression results effectively.
Regression analysis is a statistical method used to examine the relationship between a dependent variable and one or more independent variables (Uyanık & Güler, 2013: 234). It is based on the concept of fitting a regression model to the data and estimating the coefficients that represent the relationship between the variables.
The theoretical background of regression analysis is grounded in the concept of a linear relationship between variables. Linear regression assumes that there is a linear, additive relationship between the independent variables and the dependent variable. This means that the effect of the independent variables on the dependent variable can be represented by a straight line in a scatterplot.
The goal of regression analysis is to estimate the parameters (coefficients) of the linear equation that best fits the data. The most common form of linear regression is called simple linear regression, which involves one dependent variable and one independent variable. The equation for simple linear regression is:
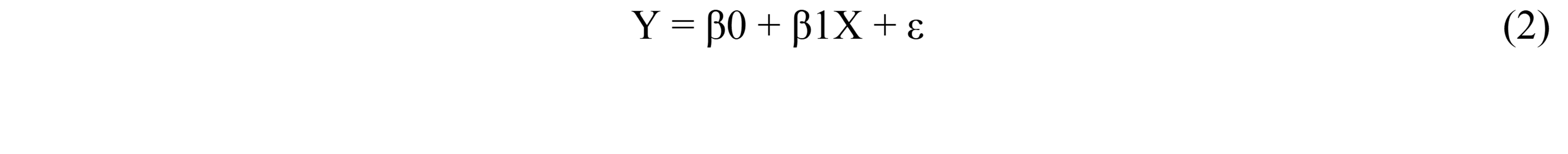
where Y is the dependent variable, X is the independent variable, β0 is the y-intercept (the value of Y when X is 0), β1 is the slope (the change in Y for a one-unit change in X), and ε is the error term (representing the variability or randomness not explained by the model).
The coefficients β0 and β1 are estimated using a method called Ordinary Least Squares (OLS), which minimizes the sum of the squared differences between the observed values of the dependent variable and the predicted values based on the regression equation (Rawlings etal., 1998: 2-4).
Multiple linear regression extends the concept of simple linear regression to include more than one independent variable. The equation becomes:
where X1, X2, ..., Xn are the independent variables, and β1, β2, ..., βn are the corresponding coefficients.
The premise is that the data points of the dependent variable, denoted as Y, are considered as random samples from populations of random variables, where the average of each population is represented by Y. To incorporate the difference between an observation Y and its population average Y, a random error is introduced into the statistical model (Rawlings etal., 1998: 2).
Regression analysis aims to estimate the coefficients (β0, β1, β2, ..., βn) that provide the best fit to the data and allow for predicting the dependent variable based on the independent variables. These coefficients indicate the direction and magnitude of the relationship between the variables. A positive coefficient suggests a positive relationship (as the independent variable increases, the dependent variable tends to increase), while a negative coefficient suggests a negative relationship.
Additionally, regression analysis allows for hypothesis testing and evaluating the statistical significance of the coefficients. Hypothesis tests such as t-tests or F-tests are used to assess whether the coefficients are significantly different from zero, indicating a meaningful relationship between the variables.
Overall, regression analysis provides a statistical framework for understanding and quantifying the relationship between variables, estimating coefficients, and making predictions based on the regression equation. It enables the identification of key factors that influence the dependent variable and aids in uncovering patterns and insights within the data.
Example 1: Predicting House Prices based on Features
Suppose you are a real estate agent and want to predict house prices based on various features such as the size of the house, the number of bedrooms, the location, and the age of the property. You collect data on recently sold houses, including information about these features and their corresponding sale prices.
To analyze the data using regression analysis, you would use a multiple linear regression model. You would treat the house price as the dependent variable and the house features (size, number of bedrooms, location, age) as independent variables. Regression analysis allows you to estimate the relationship between the independent variables and the dependent variable, providing insights into how each feature contributes to the variation in house prices. You can interpret the regression coefficients to understand the direction and magnitude of the effect of each independent variable on house prices.
Example 2: Examining the Relationship between Study Time and Exam Scores
Let's say you want to investigate the relationship between the amount of time students spend studying and their exam scores. You collect data from a group of students, recording the number of hours they spend studying and their corresponding exam scores.
To analyze the data using regression analysis, you would use a simple linear regression model. You would treat the exam score as the dependent variable and the study time as the independent variable. Regression analysis allows you to estimate the slope and intercept of the regression line, which represents the average change in the exam score associated with each additional hour of study time. By examining the coefficient of determination (R-squared value), you can determine the proportion of the variability in the exam scores that can be explained by the study time variable.
In both examples, regression analysis allows you to understand the relationship between a dependent variable and one or more independent variables. It helps you estimate the coefficients and assess the significance of the relationships, enabling predictions, and understanding the impact of the independent variables on the dependent variable.
